Draw a Circle in Axon

This commodity needs attending from an expert in mathematics. The specific problem is: In that location may be logic or math errors, complicated by the fact that this article was translated from a German original. Run across the talk page for details. WikiProject Mathematics may be able to assistance recruit an expert. (May 2017)

Graphical procedure

Axonometry is a graphical procedure belonging to descriptive geometry that generates a planar image of a three-dimensional object. The term "axonometry" ways "to measure along axes", and indicates that the dimensions and scaling of the coordinate axes play a crucial function. The upshot of an axonometric procedure is a uniformly-scaled parallel projection of the object. In general, the resulting parallel projection is oblique (the rays are non perpendicular to the paradigm airplane); only in special cases the consequence is orthographic (the rays are perpendicular to the image airplane), which in this context is called an orthogonal axonometry.

In technical cartoon and in architecture, axonometric perspective is a course of two-dimensional representation of three-dimensional objects whose goal is to preserve the impression of volume or relief. Sometimes besides chosen rapid perspective or artificial perspective, it differs from conical perspective and does not correspond what the center really sees: in particuliar parallel lines remain parallel and distant objects are not reduced in size. It can be considered a conical perspective conique whose heart has been pushed out to infinity, i.e. very far from the object observed.

The term axonometry is used both for the graphical process described below, likewise as the image produced by this procedure.

Axonometry should not exist confused with axonometric project, which in English literature usually refers to orthogonal axonometry.

Principle of axonometry [edit]

Pohlke's theorem is the basis for the following process to construct a scaled parallel projection of a 3-dimensional object:^{[1] [2]}

1. Select projections of the coordinate axes, such that all three coordinate axes are not collapsed to a single bespeak or line. Ordinarily the z-axis is vertical.
2. Select for these projections the foreshortenings, ${\displaystyle v_{ten}}$ , ${\displaystyle v_{y}}$ and ${\displaystyle v_{z}}$ , where ${\displaystyle v_{ten},v_{y},v_{z}>0.}$
3. The projection ${\displaystyle {\overline {P}}}$ of a bespeak ${\displaystyle P=(x,y,z)}$ is determined in 3 sub-steps (the result is contained of the club of these sub-steps):
4. Marking the last position as indicate ${\displaystyle {\overline {P}}}$ .

In gild to obtain undistorted results, select the projections of the axes and foreshortenings advisedly (see below). In order to produce an orthographic projection, simply the projections of the coordinate axes are freely selected; the foreshortenings are fixed (come across de:orthogonale Axonometrie).^[three]

The pick of the images of the axes and the forshortenings [edit]

Notation:

The angles can exist chosen and then that ${\displaystyle 0^{\circ }<\alpha +\beta <360^{\circ }\ .}$
The forshortenings: ${\displaystyle 0<\;v_{10},\;v_{y},\;v_{z}\ .}$

Only for suitable choices of angles and forshortenings does one get undistorted images. The next diagram shows the images of the unit of measurement cube for various angles and forshortenings and gives some hints for how to make these personal choices.

Diverse axonometric images of a unit cube. (The epitome plane is parallel to the y-z-airplane.)
The left and the far right images look more like prolonged cuboids instead of a cube.

Axonometry (cavalier perspective) of a house on checked pattern paper.

In order to keep the drawing uncomplicated, one should cull unproblematic forshortenings, for example ${\displaystyle 1.0}$ or ${\displaystyle 0.5}$ .

If ii forshortenings are equal, the project is chosen dimetric.
If the three forshortenings are equal, the projection is called isometric.
If all forshortenings are different, the projection is called trimetric.

The parameters in the diagram at right (e.one thousand. of the firm fatigued on graph paper) are: ${\displaystyle \alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {two}}\ .}$ Hence it is a dimetric axonometry. The image plane is parallel to the y-z-plane and any planar figure parallel to the y-z-plane appears in its true shape.

Special axonometries [edit]

Commonly used projections and perspectives with angles betwixt the transformed coordinate axes (α, β, γ), angles from the horizon (α _h , β _h , without γ _h = 90°) and scaling factors (v_i )

Name or property	α = ∠x̄z̄	β = ∠ȳz̄	γ = ∠x̄ȳ	α h	β h	vten	vy	5z	v
Orthogonal, orthographic, planar	90°	0°	270°	0°	270°	v		0%	any
Trimetric	90° + α h	90° + β h	360° − α − β	whatever	any	whatever	any	whatever	any
Dimetric							v
Isometric						5
Normal									100%
Oblique, clinographic				< 90°	< ninety°	any	any	any	tan(α h )
Symmetric		α	360° − 2·α	< 90°	α h				any
Equiangular	120°			thirty°
Normal, i:1 isometric						v			100%
Standard, shortened isometric									${\textstyle {\sqrt {\frac {ii}{3}}}}$ ≈ 81%
Pixel, 1:ii isometric	116.6°		126.9°	arctan(five)					fifty%
Engineering science	131.iv°	97.2°	131.4°	arccos( 3 / iv )	arcsin( i / 8 )	50%	v		100%
Cavalier	90° + α h	90°	270° − α	any	0°	any
Cabinet, dimetric cavalier						< 100%
Standard, isometric cavalier	135°		135°	45°		five
Standard 1:ii cabinet						50%	5
thirty° cabinet	116.half-dozen°		153.four°	arctan(vx )
threescore° cabinet	153.4°		116.six°	arccot(vx )
30° cavalier	120°		150°	30°		whatever
Aeriform, bird's eye view	135°		90°	45°		v		whatever	100%
Armed forces						v
Planometric	90° + α h	180° − α h		any	ninety° − α h				any
Normal planometric									100%
Shortened planometric									2 / 3 ≈ 67%

Parameters of special axonometries.

Engineer project [edit]

In this case ^{[four] [v]}

These angles are marked on many High german set squares.

Advantages of an engineer projection:

• uncomplicated forshortenings,
• a uniformly scaled orthographic projection with scaling factor ane.06,
• the contour of a sphere is a circle (in general, an ellipse) .

For more details: encounter de:Axonometrie.

Cavalier perspective, cabinet perspective [edit]

• paradigm plane parallel to y-z-plane.

In the literature the terms "cavalier perspective" and "cabinet perspective" are non uniformly defined. The to a higher place definition is the about general one. Often, further restrictions are applied.^{[6] [vii]} For example:

chiffonier perspective: additionally choose ${\displaystyle \alpha =135^{\circ }}$ (oblique) and ${\displaystyle v_{x}=0.5}$ (dimetric),

cavalier perspective: additionally choose ${\displaystyle \alpha =135^{\circ }}$ (oblique) and ${\displaystyle v_{x}=1}$ (isometric).

Birds eye view, military projection [edit]

• image plane parallel to x-y-airplane.

military projection: additionally choose ${\displaystyle v_{z}=ane}$ (isometric).

Such axonometries are ofttimes used for city maps, in social club to keep horizontal figures undistorted.

Isometric axonometry [edit]

standard isometry: cube, cuboid, house and sphere

(Non to exist confused with an isometry between metric spaces.)

For an isometric axonometry all forshortenings are equal. The angles can exist chosen arbitrarily, only a mutual choice is ${\displaystyle \alpha =\beta =\gamma =120^{\circ }}$ .

For the standard isometry or just isometry one chooses:

The reward of a standard isometry:

• the coordinates can be taken unchanged,
• the image is a scaled orthographic projection with scale gene ${\displaystyle {\sqrt {i.5}}=1.225}$ . Hence the image has a good impression and the profile of a sphere is a circle.
• Some estimator graphic systems (for example, xfig) provide a suitable raster (run across diagram) as support.

In order to prevent scaling, one can choose the unhandy forshortenings

• ${\displaystyle v_{x}=v_{y}=v_{z}={\sqrt {2/3}}}$ (instead of ane)

and the image is an (unscaled) orthographic projection.

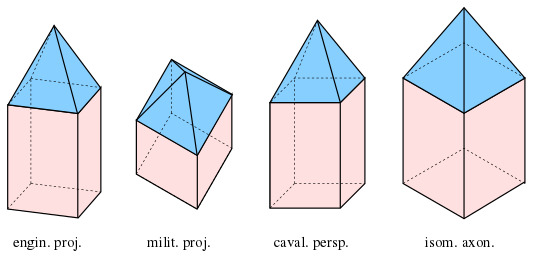
diverse axonometries of a tower
dimetric military machine projection: ${\displaystyle v_{z}=0.five,v_{x,y}=1}$ , dimetric engineering and cavalier projections: ${\displaystyle v_{x}=0.5,v_{y,z}=1}$ , isometric axonometry: ${\displaystyle v_{x,y,z}=1}$

Circles in axonometry [edit]

A parallel project of a circle is in general an ellipse. An important special example occurs, if the circle'due south aeroplane is parallel to the prototype plane–the epitome of the circle is then a congruent circle. In the diagram, the circle contained in the front end face is undistorted. If the epitome of a circle is an ellipse, one can map four points on orthogonal diameters and the surrounding square of tangents and in the image parallelogram fill-in an ellipse by hand. A better, but more fourth dimension consuming method consists of drawing the images of two perpendicular diameters of the circumvolve, which are conjugate diameters of the image ellipse, determining the axes of the ellipse with Rytz's structure and cartoon the ellipse.

• 

  Cavalier perspective: circles

• 

  Military projection: sphere

Spheres in axonometry [edit]

In a general axonometry of a sphere the image contour is an ellipse. The contour of a sphere is a circle only in an orthogonal axonometry. But, as the engineer projection and the standard isometry are scaled orthographic projections, the profile of a sphere is a circle in these cases, likewise. As the diagram shows, an ellipse every bit the profile of a sphere might exist confusing, so, if a sphere is role of an object to exist mapped, i should choose an orthogonal axonometry or an engineer project or a standard isometry.

References [edit]

• Graf, Ulrich; Barner, Martin (1961). Darstellende Geometrie. Heidelberg: Quelle & Meyer. ISBN3-494-00488-ix.
• Fucke, Kirch Nickel (1998). Darstellende Geometrie. Leipzig: Fachbuch-Verlag. ISBN3-446-00778-4.
• Leopold, Cornelie (2005). Geometrische Grundlagen der Architekturdarstellung. Stuttgart: Kohlhammer Verlag. ISBN3-17-018489-X.
• Brailov, Aleksandr Yurievich (2016). Engineering Graphics: Theoretical Foundations of Engineering science Geometry for Design. Springer. ISBN978-3-319-29717-0.
• Stärk, Roland (1978). Darstellende Geometrie. Schöningh. ISBNiii-506-37443-five.

Notes

1. ^ Graf 1961, p. 144.
2. ^ Stärk 1978, p. 156.
3. ^ Graf 1961, p. 145.
4. ^ Graf 1961, p. 155.
5. ^ Stärk 1978, p. 168.
6. ^ Graf 1961, p. 95.
7. ^ Stärk 1978, p. 159.

External links [edit]

• Orthogonal axonometry

barberboying.blogspot.com

Source: https://en.wikipedia.org/wiki/Axonometry

Share this post